Minimizing the number of instructions

As we have seen, using breadth-first search, we can find a shortest path between two points; however, the path found is not necessarily the most efficient one for Reeborg.

When it comes to moving from one point to another in the world, Reeborg uses two instructions: move() and turn_left(). An efficient path is one that minimizes the number of such instructions. We can easily adapt our algorithm to find the most efficient path. Let's review what happens when we use these two instructions:

• A move() instruction takes Reeborg from location (x, y) to location (x', y') which are next to each other on a grid. For example, if Reeborg is facing east, we will have x' == x + 1 and y' == y.
• A turn_left() instruction leaves Reeborg at the same location (x, y), but makes its direction change.

We can encode this information by using a graph with a different definition of nodes: a node will include both coordinates x and y as well as the direction in which Reeborg is facing. For example, (2, 3, "east") could be a node. For this type of graph, nodes are 3-tuples whereas before we had 2-tuples. As it turns out, we can find its neighbours using the same function as before, but calling it with an optional parameter set to True.

from search_tools import Graph
graph = Graph(turn_left=True)
neighbours = graph.neighbours((2, 3, "east"))
print(neighbours)
# If the world is empty, the result will be:
# [(3, 3, "east"), (2, 3, "north")]

You may recall that when we did not keep track of the direction, to see if we had reached the goal, we looked to see if the node we had reached was equal to the goal:

if neighbour == goal:
   return came_from

If we still do not care what direction Reeborg should be facing when reaching the goal, we need to change this to only compare the location reached. Also, to reconstruct the path, we will need to keep track of the final orientation. As a result, the above two lines of code will be changed to

if (neighbour[0], neighour[1]) == (goal[0], goal[1]):
    return came_from, neighbour

in the complete example given below.

Finally, when we used the information found when keeping only track of the required move() instructions, we had to ask Reeborg to turn until it was facing in the required direction so that a move() would take it to the next node; the code was:

for node in path:
    while node != reeborg.position_in_front():
        reeborg.turn_left()
    reeborg.move()

Now that we know explicitly which direction is required, and that nodes are connected only by a single move() or single turn_left() instruction, we need to change this to the following:

for node in path:
    _, _, direction = node
    if direction != facing(reeborg):
        reeborg.turn_left()
    else:
        reeborg.move()

All that is required is to define a function, facing(), which tells us which direction Reeborg is facing. This requires knowledge not documented in this book, nor obtainable by looking at help(UsedRobot). The following code does what is needed:

def facing(robot):
    directions = [(RUR.EAST, "east"),
                  (RUR.NORTH, "north"),
                  (RUR.WEST, "west"),
                  (RUR.SOUTH, "south")]
    for D, d in directions:
        if robot.body._orientation == D:
            return d

Putting all of this together, we end up with the following:

from search_tools import Deque, Graph
no_highlight()

def facing(robot):
    directions = [(RUR.EAST, "east"),
                  (RUR.NORTH, "north"),
                  (RUR.WEST, "west"),
                  (RUR.SOUTH, "south")]
    for D, d in directions:
        if robot.body._orientation == D:
            return d

def find_goal_bfs(start, goal, graph, no_colors=False):
    frontier = Deque(no_colors=no_colors)
    frontier.append(start)
    came_from = {start: None}

    while not frontier.is_empty():
        current = frontier.get_first()
        for neighbour in graph.neighbours(current):
            if neighbour not in came_from:
                frontier.append(neighbour)
                came_from[neighbour] = current
                if (neighbour[0], neighbour[1]) == (goal[0], goal[1]):
                    return came_from, neighbour
        frontier.mark_done(current)

# set-up
World("Empty")
think(0)
RUR.set_world_size(10, 10)
goal = 9, 9    # We do not care about the final orientation
start = 3, 3, "east"
RUR.add_final_position("house", *goal)
reeborg = UsedRobot(*start)

graph = Graph(turn_left=True)
came_from, current = find_goal_bfs(start, goal, graph, no_colors=True)

# obtain path from search result
path = []
while current != start:
    path.append(current)
    current = came_from[current]

path.reverse()

for node in path:
    _, _, direction = node
    if direction != facing(reeborg):
        reeborg.turn_left()
    else:
        reeborg.move()

In the example above, we have Reeborg facing "east". Here's the path that is found:

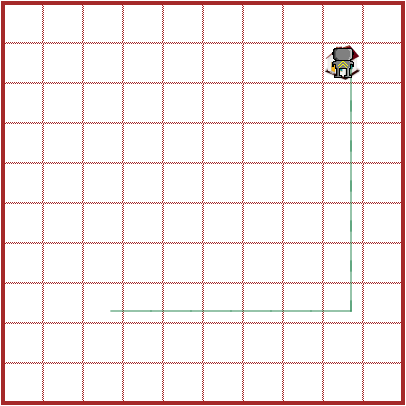
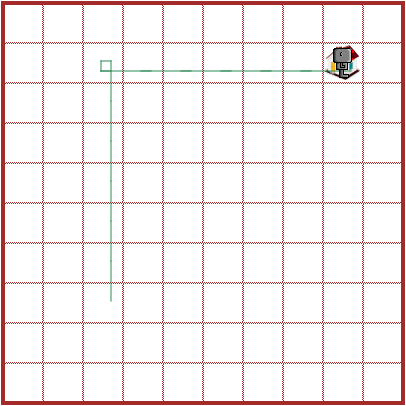
This path has a single left turn. By contrast, if we use 3, 3, "north" as the starting node, we find the following:

Using the search_tools module

For convenience, the various functions we have defined above are included in the search_tools module.

import search_tools

no_highlight()
World("Empty")
think(100)
goal = 11, 11
start = 3, 3, "east"
RUR.add_final_position("house", *goal)
reeborg = UsedRobot(*start)
RUR.add_wall("north", 11, 10)
RUR.add_wall("east", 10, 11)

graph = search_tools.Graph(turn_left=True)
came_from, current = search_tools.find_goal_bfs(start, goal, graph, no_colors=True)
path = search_tools.reconstruct_path(came_from, start, current)

for node in path:
    _, _, direction = node
    if direction != search_tools.facing(reeborg):
        reeborg.turn_left()
    else:
        reeborg.move()