Breadth-first and depth-first algorithms
[danger] The version on the website may not be compatible with the code presented here.
This will be fixed in the near future.
Both breadth-first and depth-first algorithms follow the same pattern:
- Start at a node, which is the frontier, i.e. how far we have visited so far
- Repeat until all nodes have been visited:
- Pick and remove a node from the frontier
- Add this node to the ones that have been visited
- Get this node's neighbours; any of them that have not been visited is added to the frontier
Visually, the beginning looks as follows:
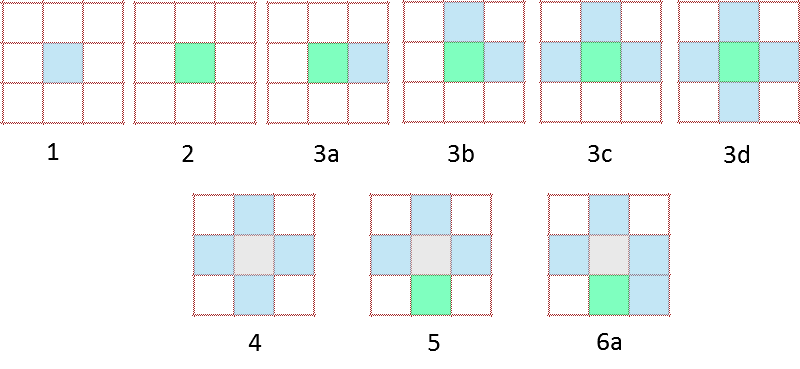
- We add a node to the frontier (node color is light blue)
- We retrieve a node added to the frontier (we have only one to choose from) and set it as the current node (green)
- a, b, c, d) we add the neighbours of the current node to the frontier.
- Having found all the neighbours, we add the original node to the visited ones (colour changed to light grey)
- We retrieve a node from the frontier (in this case, we picked the last one that was added)
- a) We add its first neighbour to the frontier; etc.
Using Python, the general algorithm looks as follows:
graph = Graph() # possibly with additional parameters
frontier = SomeDataStructure()
start = (x, y)
frontier.append(start)
visited = set([start]) # a set is the minimal Python data structure
# to keep track of visited nodes
while not frontier.is_empty():
current = frontier.GET_NODE()
# for "true" depth-first, this is where we would add a node to
# the visited set
for neighbour in graph.neighbours(current):
if neighbour not in visited:
frontier.append(neighbour)
# for "true" depth-first, we would need to break
# the loop at this point, and expand the frontier
# only one node at a time
visited.add(neighbour)
If GET_NODE() is retrieving the first node that was added to the frontier (First In, First Out, or FIFO), we have a breadth-first algorithm If GET_NODE() is retrieving the last node added to the frontier (Last In, First Out, or LIFO), we have essentially a depth-first algorithm. (A true depth-first algorithm would label a node as visited only when it is retrieved from the frontier.)
For Graph(), we'll consider two cases: either we get them always in the same order, or we get them in a random order each time.
Deque data structure
The data structure I will use for the frontier is a double ended queue or deque. I have implemented a custom deque, not as efficient as the one included in the Python standard library but one that does take care of automatically indicating which node is visited using colours, without cluttering unduly the user's code.
[info] Using a proper data structure
Deque and PriorityQueue (to be introduced later) should not be used when trying to write efficient code. Students should be taught to use proper data structures when writing their own code.
Let's first look at the cases where we select neighbours always in the same order. A complete program to do this for breadth-first search is as follows:
from search_tools import Deque, Graph
no_highlight() # highlighting would create too many frames
# however, for smaller worlds, you might want
# to leave it on and step through the program
think(0) # Makes display update as fast as possible
World("Empty")
RUR.set_world_size(11, 11)
graph = Graph(ordered=True) # <-- See comment below
frontier = Deque()
start = (6, 6)
frontier.append(start)
visited = set([start])
while not frontier.is_empty():
current = frontier.get_first() # <-- See comment below
for neighbour in graph.neighbours(current):
if neighbour not in visited:
frontier.append(neighbour)
visited.add(neighbour)
frontier.mark_done(current) # changing color only
To change from breadth-first to our quasi-depth-first, we simply need to change frontier.get_first() to frontier.get_last().
[info] Notation
There are many different implementation of double ended queues, each with its own notation for appending an item at the end of the queue, and retrieving an item either from the end or the beginning of the queue. I have chosen the following naming convention in an attempt to be clear about what is done:
append()adds an item at the end of the queue;get_last()returns the item from the end of the queue, and removes it from the queue;get_first()returns the item from the beginning of the queue, and removes it from the queue.
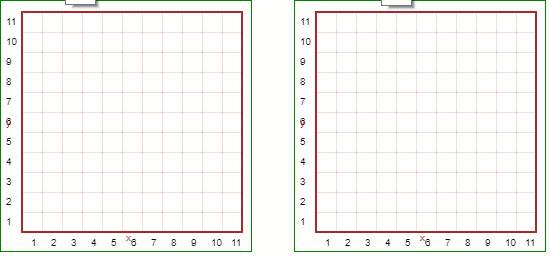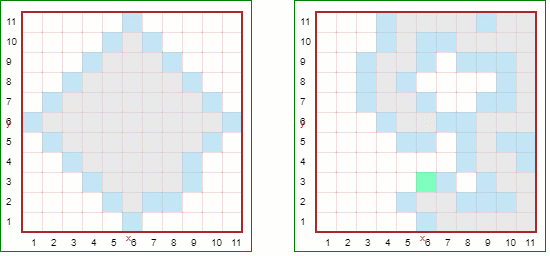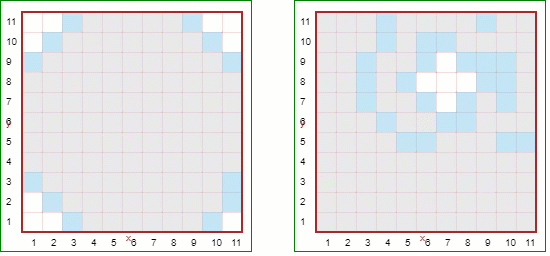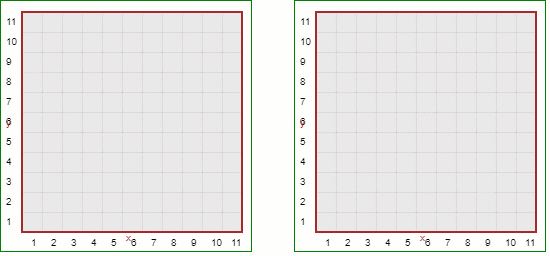
Below is a comparison of the two different algorithms,. On the left, we are using breadth-first: the frontier is expanding uniformly away from the center. For both of these, we have made a world with small tiles using RUR.get_current_world().small_tiles = True after selecting World("Empty").
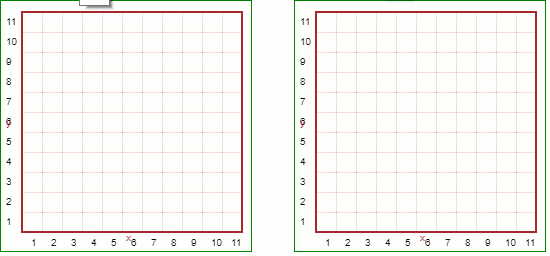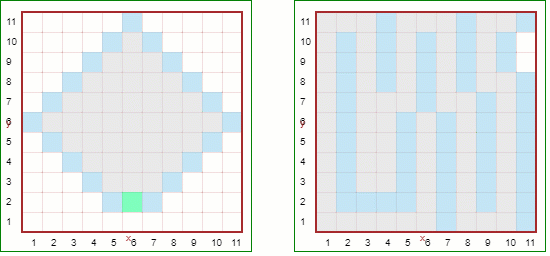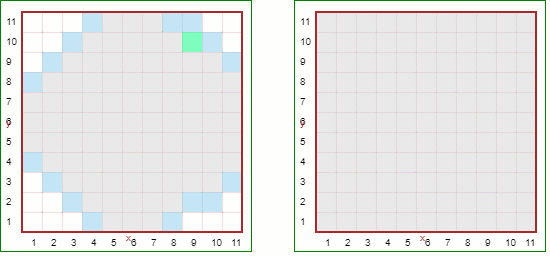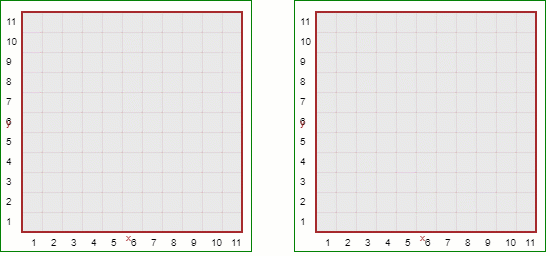
If we choose the neighbours in random order, by removing ordered=True, we get the following:
The breadth-first case does not look significantly different; however, the other case definitely does. A recursive version of a proper depth-first search algorithm with randomly ordered neighbours is what the RUR.create_maze() function uses.
Customizing the output
As usual, you can find information about Deque by importing it and using help(Deque) in Python. If you do so you will find out that you can write frontier = Deque(no_colors=True) if you wish to have no colors displayed as the algorithm is executed: this will not be useful until later, when we focus on showing only the final path after doing a search.
You can also specify custom colors using frontier.set_palette().
JavaScript version
To write a JavaScript version of the above program, we need to remember that JavaScript has neither tuples (we can use arrays instead) nor sets (we can use objects instead).
think(0);
World("Empty");
RUR.set_world_size(11, 11);
graph = new RUR.Graph({ordered: true})
frontier = new RUR.Deque();
visited = {};
start = [6, 6];
frontier.append(start);
visited[start] = true;
while (!frontier.is_empty()){
current = frontier.get_first();
neighbours = graph.neighbours(current);
for(i=0; i<neighbours.length; i++) {
neighbour = neighbours[i];
if (visited[neighbour] === undefined){
frontier.append(neighbour);
visited[neighbour] = true;
}
}
frontier.mark_done(current);
}